iFourier app for iPhone and iPad

Fourier Series and Computational Benchmarks

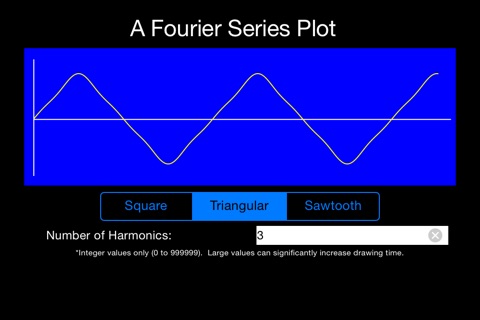
Jean Baptiste Joseph Fourier (1768-1830) was a physicist and mathematician who, among many other accomplishments, hypothesized that any periodic waveform could be generated by summing up the harmonics of sine waves. Simply put, square waves, triangular waves, saw-tooth waves and others can be generated by adding together the components using the right blend of sine wave harmonics. The “right blend” of components is expressed as a mathematical series that bears his name.

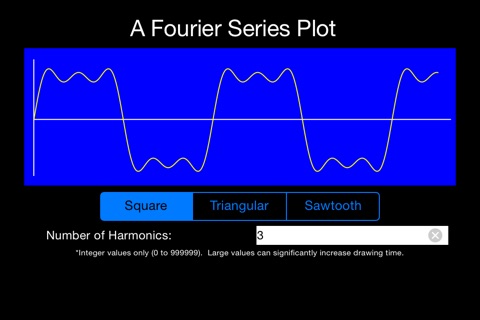
The final waveform, described with a Fourier series, is defined by manipulating the number of harmonic terms to be added together. Thus, one harmonic produces a simple sine wave. As the number of harmonics increases, the output shape becomes more and more exact. For example, use two harmonics in a Fourier series for a square wave and you can begin to see the waveform becoming “more square”. Use 300,000 terms and, for the pixel resolution of iPhones® and iPads®, you will arrive at a perfect square waveform.

Each pixel in a Fourier plot is a result of adding the number of harmonic terms desired. Thus, a Fourier series can also used as a relative measure of the computational and graphical power of an iPhone or iPad.

Imagine that a Fourier plot consists of 1000 horizontal points. If you ask for a Fourier plot that includes 2000 harmonics, then:

1000 x 2000 = 2,000,000 total mathematical calculations are made.

In other words, for each point on the plot, 2000 calculations are made and summed together. Here is the simplified equation for the first four terms, for each point in the series for a square wave.

y(t) = 4/π [ sin(2πx) + 1/3 sin(6πx) + 1/5 sin(10πx) + 1/7 sin(14πx)…]

Newer iPhones and iPads use more powerful microprocessors and thus make the necessary calculations faster. Compare the relative speed of two different iPhones® models by plotting the same waveform on both. Likewise, you can also compare the relative speed of an iPhone with an iPad. How does that new iPhone compare to a first generation iPhone?

This Fourier series application allows you to enter the number of harmonics to be used in the Fourier Series waveform generation. Integer values from 0 to 999,999 are allowed. As the number of harmonics increase, so does the computational time required to generate the waveform. For very large integer values, the computational time can be close to two minutes on older devices. One note of caution: Ever time the device is rotated or a new waveform is selected, the computations begin again. Use large integers sparingly and be ready to patiently wait for the results. As you work with this application, you will also be able to observe the computational precision of the processors used in iPhones and iPads.